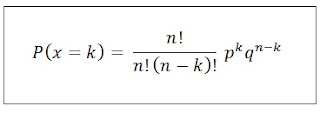Uji Binomial

Distribusi binomial adalah distribusi yang menghasilkan salah satu dari dua hasil yang saling mutually exclusive, seperti sakit-sehat, hidup-mati, sukses-gagal dan dilakukan pada percobaan yang saling independen, artinya hasil percobaan satu tidak mempengaruhi hasil percobaan lainnya (Bisma Murti, 1996). Uji binomial digunakan untuk menguji hipotesis tentang suatu proporsi populasi. Data yang cocok untuk melakukan pengujian adalah berbentuk nominal dengan dua kategori. Dalam hal ini semua nilai pengamatan yang ada di dalam populasi akan masuk dalam klasifikasi tersebut. Bila proporsi pengamatan yang masuk dalam kategori pertama adalah “sukses” = p, maka proporsi yang masuk dalam kategori kedua ”gagal” adalah 1-p = q. Uji binomial memungkinkan kita untuk menghitung peluang atau probabilitas untuk memperoleh k objek dalam suatu kategori dan n-k objek dari kategori lain. (Wahid Siulaiman, 2003).

Jika jumlah kategori pertama (P) dari satu seri pengamatan dengan n sampel adalah k, maka probabilitas untuk memperoleh P adalah:

k= jumlah objek berelemen”sukses” dari seri pengamatan berukuran n

Distribusi binomial disebut juga percobaan Bernouli, dimana percobaan Bernouli dapat dilakukan pada keadaan :

1. Setiap percobaan menghasilkan salah satu dari dua kemungkinan hasil yang saling terpisah (mutually exclusive).
2. Probabilitas “sukses (p)” adalah tetap dari satu percobaan ke percobaan lainnya.
3. Percobaan-percobaan bersifat independen, dimana hasil dari satu perobaan tidak mempengaruhi hasil percobaan lainnya.

Dengan uji binomial, pertanyaan penelitian yang akan dicari jawabannya adalah apakah kita mempunyai alasan yang cukup kuat untuk mempercayai bahwa proporsi elemen pada sampel kita sama dengan proporsi pada populasi asal sampel. Dalam prosedur uji hipoesa, distribusi binomial kita gunakan sebagai acuan dalam menetapkan besarnya probabiitas untuk memperoleh suatu nilai “kategori pertama” sebesar yang teramati dan yang lebih ekstrim dari nilai itu, dari sebuah sampel yang berasal dari populasi binomial.

Hipotesa dalam Uji Binomial
Dua sisi :   Ho: p = po dan Ha: p ≠ po
Satu sisi :  Ho: p <= po dan Ha: p > po
                Ho: p >= po dan Ha: p < po

p = proporsi pada sampel
po = proporsi pada populasi


Perhitungan Nilai p secara Manual (Bisma Murti, 1986):
Dua Sisi
Jika  p ≤ po, maka:

Jika  p > po, maka:

Satu Sisi :

Jika  Ho: p ≥  po dan   Ha: p < po, maka:

Jika Ho: p ≤ po dan Ha: p > po, maka :

 Kriteria Pengambilan Keputusan:
Untuk Uji Dua sisi:
Bila    Exact Sig. (2-tailed) < α/2 maka Ho ditolak
          Exact Sig. (2-tailed) > α/2 maka Ho gagal ditolak
 

Untuk Uji Satu sisi:
Bila    Exact Sig. (2-tailed) < α maka Ho ditolak
         Exact Sig. (2-tailed) > α maka Ho gagal ditolak

Contoh Soal :
Sebuah studi berminat melakukan uji fluorescent antibody guna meneliti adanya reaksi serum setelah pengobatan pada penderita malaria falcifarum. Dari 25 subjek yang telah disembuhkan, 15 subjek ditemukan bereaksi positif. Jika sampel itu memenuhi semua asumsi yang mendasari uji binomial, dapatkah kita menyimpulkan dari data itu bahwa proporsi reaksi positif dalam populasi yang bersangkutan adalah lebih besar dari 0,5? Misalkan α = 0,05 (Wayne W.Daniel, 2003, hal 67).

HIPOTESA
Ho : p ≤ 0,5 dan Ha: p > 0,5

PERHITUNGAN

 Dari tabel binomial, dengan n=25, x-1=14 dan Po=0,5, untuk uji satu sisi dengan P = 15/25 = 0,6 > po =0,5, diperoleh nilai p :

                                           14         25!

            p=P(X ≥ 15) =  1 - ∑ --------------  0,5^k 0,5^25-k 

                                             k=0   25! (25-k)!

 
                                = 1 – 0,7878 = 0,2122

Karena p = 0,2122 > 0,05. maka Ho gagal ditolak, sehingga kita dapat menyimpulkan bahwa proporsi reaksi serum di antara populasi yang telah mendapat pengobatan malaria tidak dapat dikatakan lebih besar secara bermakna dari 0,5.

Blog Biostatistik : http://statistik-kesehatan.blogspot.com/2011/04/uji-binomial.html